Data_structures_BaseDataType

Data_structures_BaseDataType

Slience_Displace Lv2
  2024-11-28 2024-11-28 00 Created   2024-12-19 17:33:01 2024-12-19 17:33 Updated      12.2k Words  53 Mins  

Data_structures_BaseDataType

本文代码采用C语言编写,用到了部分Cpp语法,详见 C_NOTE 的Cpp引用部分

由于每种数据结构各种操作需要相互协同工作才能起作用,总体代码长度过长,不方便阅读,故此我决定将不同操作分开讲解,并在章节最后附上整体的代码 (其实就是合到一起)

时间复杂度&空间复杂度

时间复杂度(time complexity)

时间复杂度是指算法执行所需时间的量度，通常以输入规模 的函数形式表示。它反映了算法的运行时间如何随着输入规模的增加而变化。

  • ：常数时间复杂度，与输入规模无关，执行时间固定。
  • ：线性时间复杂度，时间与输入规模成正比，如遍历数组。
  • ：对数时间复杂度，适合分治法（如二分查找）。
  • ：平方时间复杂度，常见于嵌套循环

通常我们观察一段代码的运行次数来判断它的时间复杂度

1
2
3
4
def example(arr):
    for i in range(len(arr)):
        for j in range(len(arr)):
            print(arr[i] + arr[j])

外层循环运行 次，内层循环也运行 次，因此时间复杂度为

空间复杂度(space complexity)

常见情况

  • ：仅使用常数空间，通常为变量或指针的操作，如简单循环。
  • ：需要存储所有输入元素的大小空间，如线性数组。
  • ：需要矩阵或二维表结构的空间，如图论算法。

计算空间复杂度的步骤

  1. 识别固定存储：如函数内的常量。
  2. 计算辅助结构：例如数组、栈、队列。
  3. 加和取上限：得到整体复杂度。

高效算法应在降低时间复杂度的前提下尽量减少空间开销

线性表

线性表（Linear List）是计算机科学中一种常见的数据结构，用来表示元素按顺序排列的一组数据。在线性表中，数据元素之间存在一对一的线性关系，即每个数据元素有且仅有一个直接前驱和一个直接后继（第一个和最后一个元素除外）。线性表可用于各种场景，包括队列、栈、链表等

顺序表(Sequence List)

顺序表 (Sequnce List) 使用一块连续的内存空间来存储线性表的数据元素。每个元素的存储位置可以通过一个下标直接访问,其本质是一个数组。

  • 优点：

    • 支持快速的随机访问，可以通过下标直接访问任何位置的元素。
    • 空间利用率较高，不需要额外的存储空间。

  • 缺点：

    • 插入和删除元素的操作效率较低，涉及大量元素的移动。
    • 顺序存储的大小固定，无法动态扩展。

1. 顺序表的静态定义 :

包含一个数组 和 一个用来记录当前顺序表长度的int变量

1
2
3
4
5
6
7
8
9
typedef int ElemType;  //将顺序表的值类型另命名，方便后续修改数据类型类型

//定义顺序表
typedef struct
{
	ElemType data[MaxSize]; //线性表本质是一个数组,被人为的添加了逻辑顺序和排序长度
	int length; //当前顺序表中有多少个元素
}SqList;

2.插入 :

从插入位置开始，将后续元素依次向后移动，腾出插入位置

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
// 在排序表第i个位置添加元素  //排序表从1开始  //索引表从0开始
bool ListInsert(SqList& L, int i, ElemType element) 
{
	//参数归一化,方便后续操作
	int i_index = i - 1; //将参数从排序表转换为索引表
	int length_index = L.length - 1; //将参数从排序表长度转换为末端索引值

	if (i_index < 0 || i_index > length_index)  //判断i是否合法,
	{
		printf("the position of i is illegal , change it to less than L.length\n");
		return false;
	}
	if (length_index == MaxSize)   //存储空间满了则无法继续插入值
	{
		printf("MaxSize cannot insert value\n");
		return false;
	}

	L.length++; //因为要加入一个新元素,故长度加一
	length_index = L.length - 1; //由于L.length发生了变化,需更新length_index

	for (int j = length_index; j >= i_index; j--) //根据索引
	{
		L.data[j] = L.data[j - 1];
	}
	L.data[i_index] = element;
	
}

3.删除 :

从删除位置开始，将后续元素向前移动

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
//指定元素值删除首个符合条件的元素  //若想删除所有的同一元素,则只需循环调用此函数即可
bool DelteElement_by_value(SqList& L, ElemType element)
{
	int j = -1; //初始化j,否则无法作为左操作数输入将其他变量的值赋予j
	for (int i = 0; i < L.length-1; i++)//获取第一个符合目标元素值的索引值
	{
		if (element == L.data[i])
		{
			j = i;
			break;
		}
	}

	// 若未找到元素，返回 false
	if (j == -1) {
		printf("Element not found.\n");
		return false;
	}

	for (int i = j; i < L.length - 1; i++)
	{
		L.data[i] = L.data[i + 1];
	}
	L.length--;
	return true;
}


//指定排序位置删除元素
bool DelteElement_by_position(SqList& L, int i)
{
	//参数归一化,方便后续操作
	int i_index = i - 1; //将参数从排序表转换为索引表
	int length_index = L.length - 1; //将参数从排序表长度转换为末端索引值

	if (i_index < 0 || i_index > length_index)  //判断i是否合法,
	{
		printf("the position of i is illegal , change it to less than L.length\n");
		return false;
	}

	for (int i = i_index; i < L.length - 1; i++)
	{
		L.data[i] = L.data[i + 1];
	}
	L.length--;
	return true;
}

4.查找 :

直接通过下标访问目标位置元素

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
//根据值查找该值所在的首个排序位置
int SerchFirstPosition_by_value(SqList& L, ElemType element)
{
	int j = -1; //初始化j,否则无法作为左操作数输入将其他变量的值赋予j
	for (int i = 0; i < L.length - 1; i++)//获取第一个符合目标元素值的排序位置
	{
		if (element == L.data[i])
		{
			j = i + 1;
			break;
		}
	}

	// 若未找到元素，返回 false
	if (j == -1) 
	{
		printf("Element not found.\n");
	}

	printf("the first position of value:%d is %d\n", element,j);
	return j;

}


//根据值查找该值所在的所有排序位置
int SerchAllPositions_by_value(SqList& L, ElemType element)
{
	int j = -1; //初始化j,否则无法作为左操作数输入将其他变量的值赋予j
	for (int i = 0; i <= L.length-1; i++)//获取第一个符合目标元素值的排序位置
	{
		if (element == L.data[i])
		{
			j = i + 1;
			printf("the position of value:%d is %d\n", element, j);
		}
	}

	// 若未找到元素，返回 false
	if (j == -1)
	{
		printf("The Element of %d is not found.\n", element);
	}	
	return 0;
}

顺序表总体代码

顺序表 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
#include <stdio.h>

#define MaxSize 50

typedef int ElemType;  //将顺序表的值类型另命名，方便后续修改数据类型类型

//定义顺序表
typedef struct
{
	ElemType data[MaxSize]; //线性表本质是一个数组,被人为的添加了逻辑顺序和排序长度
	int length; //当前顺序表中有多少个元素
}SqList;


// 在排序表第i个位置添加元素  //排序表从1开始  //索引表从0开始
bool ListInsert(SqList& L, int i, ElemType element) 
{
	//参数归一化,方便后续操作
	int i_index = i - 1; //将参数从排序表转换为索引表
	int length_index = L.length - 1; //将参数从排序表长度转换为末端索引值

	if (i_index < 0 || i_index > length_index)  //判断i是否合法,
	{
		printf("the position of i is illegal , change it to less than L.length\n");
		return false;
	}
	if (length_index == MaxSize)   //存储空间满了则无法继续插入值
	{
		printf("MaxSize cannot insert value\n");
		return false;
	}

	L.length++; //因为要加入一个新元素,故长度加一
	length_index = L.length - 1; //由于L.length发生了变化,需更新length_index

	for (int j = length_index; j >= i_index; j--) //根据索引
	{
		L.data[j] = L.data[j - 1];
	}
	L.data[i_index] = element;
	
}


//指定元素值删除首个符合条件的元素  //若想删除所有的同一元素,则只需循环调用此函数即可
bool DelteElement_by_value(SqList& L, ElemType element)
{
	int j = -1; //初始化j,否则无法作为左操作数输入将其他变量的值赋予j
	for (int i = 0; i < L.length-1; i++)//获取第一个符合目标元素值的索引值
	{
		if (element == L.data[i])
		{
			j = i;
			break;
		}
	}

	// 若未找到元素，返回 false
	if (j == -1) {
		printf("Element not found.\n");
		return false;
	}

	for (int i = j; i < L.length - 1; i++)
	{
		L.data[i] = L.data[i + 1];
	}
	L.length--;
	return true;
}


//指定排序位置删除元素
bool DelteElement_by_position(SqList& L, int i)
{
	//参数归一化,方便后续操作
	int i_index = i - 1; //将参数从排序表转换为索引表
	int length_index = L.length - 1; //将参数从排序表长度转换为末端索引值

	if (i_index < 0 || i_index > length_index)  //判断i是否合法,
	{
		printf("the position of i is illegal , change it to less than L.length\n");
		return false;
	}

	for (int i = i_index; i < L.length - 1; i++)
	{
		L.data[i] = L.data[i + 1];
	}
	L.length--;
	return true;
}


//根据值查找该值所在的首个排序位置
int SerchFirstPosition_by_value(SqList& L, ElemType element)
{
	int j = -1; //初始化j,否则无法作为左操作数输入将其他变量的值赋予j
	for (int i = 0; i < L.length - 1; i++)//获取第一个符合目标元素值的排序位置
	{
		if (element == L.data[i])
		{
			j = i + 1;
			break;
		}
	}

	// 若未找到元素，返回 false
	if (j == -1) 
	{
		printf("Element not found.\n");
	}

	printf("the first position of value:%d is %d\n", element,j);
	return j;

}


//根据值查找该值所在的所有排序位置
int SerchAllPositions_by_value(SqList& L, ElemType element)
{
	int j = -1; //初始化j,否则无法作为左操作数输入将其他变量的值赋予j
	for (int i = 0; i <= L.length-1; i++)//获取第一个符合目标元素值的排序位置
	{
		if (element == L.data[i])
		{
			j = i + 1;
			printf("the position of value:%d is %d\n", element, j);
		}
	}

	// 若未找到元素，返回 false
	if (j == -1)
	{
		printf("The Element of %d is not found.\n", element);
	}	
	return 0;
}

//打印列表
void PrintList(SqList L)
{
for (size_t i = 0; i < L.length; i++)
{
	printf("%3d", L.data[i]);
}
printf("\n-------length=%d---------\n", L.length);
printf("\n");
}

int main()
{
	SqList L;
	L.data[0] = 1; //向顺序表中添加数值
	L.data[1] = 7;
	L.data[2] = 2;
	L.data[3] = 3;
	L.data[4] = 5;
	L.data[5] = 7;

	L.length = 6; //设置长度

	PrintList(L);

	//ListInsert(L, 3, 99);
	//PrintList(L);

	//ListInsert(L, 7, 90);
	//PrintList(L);

	//DelteElement_by_value(L,7);
	//PrintList(L);

	//DelteElement_by_position(L, 4);
	//PrintList(L);

	//SerchFirstPosition_by_value(L, 7);

	SerchAllPositions_by_value(L, 88);

	return 0;
}

单链表(Single Linked List)

单链表是一种链式数据结构，用于存储一组节点。每个节点包含数据域和指针域，其中：

  1. 数据域（Data Field）：存储节点的数据。
  2. 指针域（Next Field）：存储指向下一个节点的指针。

注意,这里构造的单链表头节点内无值,但因visual studio2022会自动在输出时为空的值域填充随机值,故用我们这里NULL即0填充,在实际使用链表时头节点会被填充数据,写入链表长度或其他数值信息

我改主意了,头节点数据填入链表长度

在链表中,节点的概念是逻辑性的虚拟的,实际代码层面只存在包含于构造体中的指针和数据

1.创建单链表

包含数据域 和 指针域,指针用于指向下一个结构体(节点)

1
2
3
4
5
6
7
typedef int ElementType;

typedef struct LNode{
	ElementType data;  //数据域
	LNode* next;  //指向结构体LNode的指针  
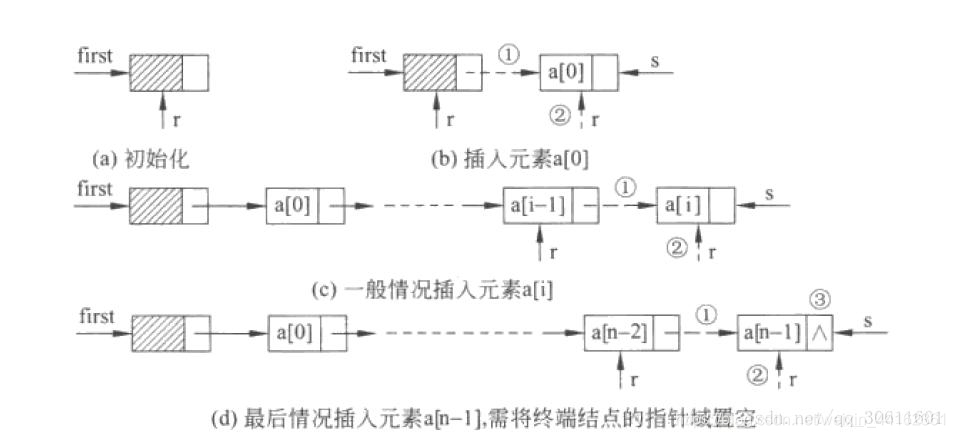
}LNode,*LinkList;   //定义链表的名字和头指针  //*LinkList表示LinkList是一个指针变量，指向结构体LNode的首地址
//LNode* 和 LinkList 都可以表示结构体LNode的首地址

2.头插法添加节点

头插法是一种在链表头部插入节点的方式，适用于倒序建立链表。步骤如下：

  1. 为新节点分配内存。
  2. 设置新节点的数据值。
  3. 将新节点的 next 指针指向当前的头节点。
  4. 更新头指针，使其指向新节点。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
//头插法，将新结点插入到链表的头部
void List_head_insert(LinkList &L)
{
	LNode* s; //定义一个指针变量s，指向新结点
	ElementType x = 0; //定义一个变量x，用于输入数据

	//创建头结点
	L = (LinkList)malloc(sizeof(LNode));  //分配内存给链表的头结点,malloc申请内存后返回首地址给到L,则L为结构体LNode的首地址(即头指针)
	L->data = x;  //头结点的data域置0
	L->next = nullptr;

	
	//头插法，将新结点插入到链表的头部
	scanf_s("%d", &x);//首次输入数据
	while(x != 9999) 
	{
		s = (LinkList)malloc(sizeof(LNode));  //分配内存给新结点		
		s->data = x; //给新结点赋值
		s->next = L->next; //新结点的指针域指向旧头结点
		L->next = s; //将头结点的指针域指向新结点

		scanf_s("%d", &x);//再次输入数据,直到输入9999结束
	}
}
int main()
{
	LinkList L; //定义链表的头指针.L为结构体类型的指针变量，指向结构体LNode的头节点地址
}

3.尾插法添加节点

尾插法是将新节点添加到链表尾部，适用于顺序建立链表。步骤如下：

  1. 为新节点分配内存。
  2. 设置新节点的数据值。
  3. 将当前尾节点的 next 指针指向新节点。
  4. 更新尾节点，使其指向新节点
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
//尾插法，将新结点插入到链表的尾部
void List_tail_insert(LinkList& L)
{
	LNode* s,*r; //定义一个指针变量s，指向新结点
	ElementType x = 0; //定义一个变量x，用于输入数据
	//创建头结点
	L = (LinkList)malloc(sizeof(LNode));  //分配内存给链表的头结点,malloc申请内存后返回首地址给到L,则L为结构体LNode的首地址(即头指针)
	L->data = x;  //头结点的data域置0
	L->next = nullptr;
	r = L; //r指向头结点

	scanf_s("%d", &x);
    //尾插法，将新结点插入到链表的尾部
	while(x != 9999)
	{ 
		s = (LinkList)malloc(sizeof(LNode));
		s->data = x; //给新结点赋值
		r->next =s; //将r的指针域指向新结点,在第一次循环时,相当于让L的指针域指向新结点,以为上文定义了*r =L
		r = s; //r指向新结点
		scanf_s("%d", &x);//输入数据
	}
	r->next = nullptr; //最后一个结点的指针域置空
}
int main()
{
	LinkList L; //定义链表的头指针.L为结构体类型的指针变量，指向结构体LNode的头节点地址
}

5.单链表查询

  1. 定义计数器变量
  2. 考虑非法参数并给出返回值
  3. 用while循环从头节点开始遍历链表,由计数器控制步数
  4. 考虑查找失败结果
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
//按位置查找结点
LNode* List_search_position(LinkList L, int serch_position)
{
	int i = 0; //定义一个变量i，用于记录当前结点的位置
	if (serch_position < 1) //如果serch_position小于1,则返回空指针
	{
		printf("serch_position is less than 1,i will return head pointer,it means the serch_position is 1\n");
		return L;
	}
	if (serch_position > L->data) //如果serch_position大于链表的长度,则返回空指针
	{
		printf("serch_position is greater than the length of the list\n");
		return nullptr;
	}

	while (L != nullptr && i != serch_position)//当L不为空且i不等于serch_position时,遍历链表
	{
		L = L->next; //L指向下一个结点
		i++; 
	}

	if(i != serch_position) //如果循环完毕后,i不等于serch_position,则说明没有找到serch_position位置的结点
	{
		printf("The serch_position is not found,it may because the serch_position is greater than the length of the list\n");
		return nullptr;
	}
	return L; //返回目标结点的指针
}

//按值查找结点
LNode* List_search_value(LinkList L, ElementType x)
{
	while (L != nullptr && L->data != x) //当L不为空且L的data域不等于x时,循环
	{
		L = L->next; //L指向下一个结点
	}
	if (L != nullptr) //如果L不为空,则返回L
	{
		return L;  //当循环完毕后,如果L不为空且L的data域等于x,则说明找到了x值对应的结点 //返回找到的结点
	}
	else //如果L为空,则说明没有找到x值对应的结点
	{
		printf("The value is not found\n");
		return nullptr;
	}
}
int main()
{
	LinkList Serch_pointer;//定义指针变量，指向要查找的结点
}

6.按位置插入节点

  1. 定义一个指针变量s，用于指向新结点
  2. 考虑在第一个位置插入的结点的情况，此时直接应用头插法算法
  3. 通过List_search_position(L, insert_position - 1)获取目标结点的前一个结点的指针域的值
  4. 判断p是否为空，决定是否执行插入算法
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
//按位置插入结点到第insert_position个位置
bool List_insert_position(LinkList L, int insert_position, ElementType x)
{
	
	LinkList s; //定义一个指针变量s，用于指向新结点
	if (insert_position == 1) {
		s = (LinkList)malloc(sizeof(LNode));  //分配内存给新结点
		s->data = x; //给新结点赋值
		s->next = L->next; //新结点的指针域指向旧头结点
		L->next = s; //将头结点的指针域指向新结点
		return true;
	}

	LinkList p = List_search_position(L, insert_position - 1);//p指向insert_position位置的结点，即p的值为目标结点的前一个结点的指针域的值
	if (p == nullptr) //如果s为空,则说明insert_position大于链表的长度,插入到尾结点之后
	{
		printf("insert_position is greater than the length of the list,you can't insert it\n");
		return false;
	}
	else
	{
		s = (LinkList)malloc(sizeof(LNode));  //分配内存给新结点
		s->data = x; //给新结点赋值
		s->next = p->next; //新结点的指针域指向旧结点的下一个结点
		p->next = s; //将旧结点的指针域指向新结点
	}
}

7.单链表删除节点

  1. 通过List_search_position(L, insert_position - 1)获取目标结点的前一个结点的指针域的值
  2. 判断p是否为空，决定是否执行删除算法
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
//按位置删除指定结点
bool List_delete_position(LinkList &L, int delete_position)
{ 
	LinkList p = List_search_position(L, delete_position - 1); //p指向要删除的结点
	if (p == nullptr) //如果p为空,则说明delete_position大于链表的长度,删除失败
	{
		printf("delete_position is greater than the length of the list,you can't delete it\n");
		return false;
	}
	else
	{
		LinkList q; //定义一个指针变量q，用于储存被删除结点的地址
		q = p->next; //q获得了目标节点的指针域的值
		p->next = q->next; //将p的指针域指向q的下一个结点
		free(q); //释放要删除的结点
		return true;
	}
}

单链表总体代码

单链表总体代码 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
#include <stdio.h>
#include <stdlib.h>
#include <string.h>

typedef int ElementType;

typedef struct LNode{
	ElementType data;  //数据域
	LNode* next;  //指向结构体LNode的指针  
}LNode,*LinkList;   //定义链表的名字和头指针  //*LinkList表示LinkList是一个指针变量，指向结构体LNode的首地址
//LNode* 和 LinkList 都可以表示结构体LNode的首地址


//头插法，将新结点插入到链表的头部
void List_head_insert(LinkList &L)
{
	LNode* s; //定义一个指针变量s，指向新结点
	ElementType x = 0; //定义一个变量x，用于输入数据

	//创建头结点
	L = (LinkList)malloc(sizeof(LNode));  //分配内存给链表的头结点,malloc申请内存后返回首地址给到L,则L为结构体LNode的首地址(即头指针)
	//L->data = x;  //头结点的data域置0
	L->data = 99;  //头结点的data域置为链表长度,注意这里的99是随便设置的,具体取值要根据链表实际长度来确定
	L->next = nullptr;

	
	//头插法，将新结点插入到链表的头部
	scanf_s("%d", &x);//首次输入数据
	while(x != 9999) 
	{

		s = (LinkList)malloc(sizeof(LNode));  //分配内存给新结点		
		s->data = x; //给新结点赋值
		s->next = L->next; //新结点的指针域指向旧头结点
		L->next = s; //将头结点的指针域指向新结点

		scanf_s("%d", &x);//再次输入数据,直到输入9999结束

	}


}


//尾插法，将新结点插入到链表的尾部
void List_tail_insert(LinkList& L)
{
	LNode* s,*r; //定义一个指针变量s，指向新结点    r，指向最后一个结点
	ElementType x = 0; //定义一个变量x，用于输入数据
	//创建头结点
	L = (LinkList)malloc(sizeof(LNode));  //分配内存给链表的头结点,malloc申请内存后返回首地址给到L,则L为结构体LNode的首地址(即头指针)
	//L->data = x;  //头结点的data域置0
	L->data = 99;  //头结点的data域置为链表长度,注意这里的99是随便设置的,具体取值要根据链表实际长度来确定
	L->next = nullptr;
	r = L; //r指向头结点

	scanf_s("%d", &x);
    //尾插法，将新结点插入到链表的尾部
	while(x != 9999)
	{ 
		s = (LinkList)malloc(sizeof(LNode));
		s->data = x; //给新结点赋值
		r->next =s; //将r的指针域指向新结点,在第一次循环时,相当于让L的指针域指向新结点,以为上文定义了*r =L
		r = s; //r指向新结点
		scanf_s("%d", &x);//输入数据
	}
	r->next = nullptr; //最后一个结点的指针域置空
}


//按位置查找结点
LNode* List_search_position(LinkList L, int serch_position)
{
	int i = 0; //定义一个变量i，用于记录当前结点的位置
	if (serch_position < 1) //如果serch_position小于1,则返回空指针
	{
		printf("serch_position is less than 1,i will return head pointer,it means the serch_position is 1\n");
		return L;
	}
	if (serch_position > L->data) //如果serch_position大于链表的长度,则返回空指针
	{
		printf("serch_position is greater than the length of the list\n");
		return nullptr;
	}

	while (L != nullptr && i != serch_position)//当L不为空且i不等于serch_position时,遍历链表
	{
		L = L->next; //L指向下一个结点
		i++; 
	}

	if(i != serch_position) //如果循环完毕后,i不等于serch_position,则说明没有找到serch_position位置的结点
	{
		printf("The serch_position is not found,it may because the serch_position is greater than the length of the list\n");
		return nullptr;
	}
	return L; //返回目标结点的指针
}



//按值查找结点
LNode* List_search_value(LinkList L, ElementType x)
{
	while (L != nullptr && L->data != x) //当L不为空且L的data域不等于x时,循环
	{
		L = L->next; //L指向下一个结点
	}
	if (L != nullptr) //如果L不为空,则返回L
	{
		return L;  //当循环完毕后,如果L不为空且L的data域等于x,则说明找到了x值对应的结点 //返回找到的结点
	}
	else //如果L为空,则说明没有找到x值对应的结点
	{
		printf("The value is not found\n");
		return nullptr;
	}
}


//按位置插入结点到第insert_position个位置
bool List_insert_position(LinkList L, int insert_position, ElementType x)
{
	
	LinkList s; //定义一个指针变量s，用于指向新结点
	if (insert_position == 1) {
		s = (LinkList)malloc(sizeof(LNode));  //分配内存给新结点
		s->data = x; //给新结点赋值
		s->next = L->next; //新结点的指针域指向旧头结点
		L->next = s; //将头结点的指针域指向新结点
		return true;
	}

	LinkList p = List_search_position(L, insert_position - 1);//p指向insert_position位置的结点，即p的值为目标结点的前一个结点的指针域的值
	if (p == nullptr) //如果s为空,则说明insert_position大于链表的长度,插入到尾结点之后
	{
		printf("insert_position is greater than the length of the list,you can't insert it\n");
		return false;
	}
	else
	{
		s = (LinkList)malloc(sizeof(LNode));  //分配内存给新结点
		s->data = x; //给新结点赋值
		s->next = p->next; //新结点的指针域指向旧结点的下一个结点
		p->next = s; //将旧结点的指针域指向新结点
	}

}


//按位置删除指定结点
bool List_delete_position(LinkList &L, int delete_position)
{ 
	LinkList p = List_search_position(L, delete_position - 1); //p指向要删除的结点
	if (p == nullptr) //如果p为空,则说明delete_position大于链表的长度,删除失败
	{
		printf("delete_position is greater than the length of the list,you can't delete it\n");
		return false;
	}
	else
	{
		LinkList q; //定义一个指针变量q，用于储存被删除结点的地址
		q = p->next; //q获得了目标节点的指针域的值
		p->next = q->next; //将p的指针域指向q的下一个结点
		free(q); //释放要删除的结点
		return true;
	}
}


//打印链表
void List_print(LinkList L)
{
	while(L != nullptr)
	{
		printf("%d ", L->data);
		L = L->next;
	}
	printf("\n");
}	



int main()
{
	LinkList L; //定义链表的头指针.L为结构体类型的指针变量，指向结构体LNode的头节点地址
	LinkList Serch_pointer;//定义指针变量，指向要查找的结点

	List_head_insert(L);

	//List_tail_insert(L);

	List_print(L);

	Serch_pointer = List_search_position(L, 1); //查找第3个结点
	printf("The data of the serch_pointer is %d\n", Serch_pointer->data);

	//Serch_pointer = List_search_value(L, 10); //查找值为10的结点
	//printf("The data of the serch_pointer is %d and the value is %d\n", L, Serch_pointer->data);
	////打印指针没有实际意义，只是为了测试指针是否存在,层序每次运行的结果都不一样，所以指针的值也是随机的

	//List_insert_position(L, 1, 100); //在第3个位置插入值为100的结点
	//List_print(L);

	List_delete_position(L, 1); //删除第3个结点
	List_print(L);

	return 0;
}

栈 （Stack）

栈是一种后进先出（LIFO）的数据结构。栈中元素只能在一端添加或移除，这一端被称为“栈顶”。在栈的操作中，常用的操作有：

  • push：将元素压入栈顶。
  • pop：将栈顶元素弹出。
  • peek：查看栈顶元素，但不移除它。

栈的应用：广泛用于递归算法、表达式求值、括号匹配、函数调用等场景。

栈的本质为人为控制进出规则的数组,通过控制索引来控制数组中的数据进出，栈可以顺序定义也可链式定义

顺序栈(squencial stack)

有顺序表发展而来的数据结构，其在内存中需要连续的空间

1.顺序栈结构定义

顺序栈由一个数组和一个用于标记数组索引的整型值组成

1
2
3
4
5
6
7
8
9
10
11
12
13
14
#define MAX_SIZE 100
typedef int ElementType;

//顺序栈(squencial stack)结构定义
typedef struct Stack
{
	ElementType data[MAX_SIZE];//栈体
	int top;//栈顶索引
}SqStack;

int main()
{
	SqStack S;
}

2.初始化栈

1
2
3
4
void InitStack(SqStack& S)
{
	S.top = -1;//栈顶索引初始化为-1,表示栈为空 同时意味着栈索引从0开始
}

3.入栈操作(Push)

  1. 判断是否可继续入栈
  2. 修改索引，填值
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
//判断栈是否为满
bool IsStackFull(SqStack S)
{
	if (S.top == MAdata_x_SIZE - 1)
	{
		printf("Stack is full!\n");
		return false;
	}
	else
		return true;
}

//入栈操作(Push)
bool Push(SqStack& S, ElementType data_x)
{
	if (IsStackFull(S))
	{
		//S.top++;
		//S.data[S.top] = data_x; //该代码可被优化

		S.data[++S.top] = data_x; //优化后代码  其中[++S.top]表示S.data索引自增1，然后将data_x值存入栈顶
		return true;
	}
	else
	{
		return false;
	}
}

4.出栈操作(Pop)

  1. 判断栈内是否有值
  2. 取值，修改索引
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
//出栈操作(Pop)(获取栈顶元素并删除栈内的栈顶元素)
bool Pop(SqStack& S, ElementType& data_x)
{
	if (S.top == -1)
	{
		printf("Stack is empty,can not pop!\n");
		return false;
	}
	else
	{
		//data_x = S.data[S.top];
		//S.top--;
		data_x = S.data[S.top--]; //优化后代码  其中[S.top--]表示S.data先调用索引为[S.top]的值后,再将索引自减1，然后取出栈顶元素值
		return true;
	}
}//出栈本质为索引向前移动

5.读取栈顶元素(Peek)

  1. 判断栈内是否有值
  2. 取值
1
2
3
4
5
6
7
8
9
10
11
12
13
14
//读取栈顶元素(Peek)
bool Peek(SqStack& S, ElementType& data_x)
{
	if (S.top == -1)
	{
		printf("Stack is empty,can not get top!\n");
		return false;
	}
	else
	{
		data_x = S.data[S.top];
		return true;
	}	
}

顺序栈总体代码

顺序栈总体代码 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
#include <stdio.h>
#include <stdlib.h>
#include <string.h>


#define MAdata_x_SIZE 8
typedef int ElementType;

//顺序栈(squencial stack)结构定义
typedef struct Stack
{
	ElementType data[MAdata_x_SIZE];
	int top; //栈顶索引
}SqStack;

//初始化栈
void InitStack(SqStack& S)
{
	S.top = -1;//栈顶索引初始化为-1,表示栈为空 同时意味着栈索引从0开始
}

//判断栈是否为满
bool IsStackFull(SqStack S)
{
	if (S.top == MAdata_x_SIZE - 1)
	{
		printf("Stack is full!\n");
		return false;
	}
	else
		return true;
}

//入栈操作
bool Push(SqStack& S, ElementType data_x)
{
	if (IsStackFull(S))
	{
		//S.top++;
		//S.data[S.top] = data_x; //该代码可被优化

		S.data[++S.top] = data_x; //优化后代码  其中[++S.top]表示S.data索引自增1，然后将data_x值存入栈顶
		return true;
	}
	else
	{
		return false;
	}
}


//出栈操作(获取栈顶元素并删除栈内的栈顶元素)
bool Pop(SqStack& S, ElementType& data_x)
{
	if (S.top == -1)
	{
		printf("Stack is empty,can not pop!\n");
		return false;
	}
	else
	{
		//data_x = S.data[S.top];
		//S.top--;
		data_x = S.data[S.top--]; //优化后代码  其中[S.top--]表示S.data先调用索引为[S.top]的值后,再将索引自减1，然后取出栈顶元素值
		return true;
	}
}//出栈本质为索引向前移动

//读取栈顶元素
bool GetTop(SqStack& S, ElementType& data_x)
{
	if (S.top == -1)
	{
		printf("Stack is empty,can not get top!\n");
		return false;
	}
	else
	{
		data_x = S.data[S.top];
		return true;
	}	
}


//输出栈
void PrintStack(SqStack S)
{
	if (S.top == -1)
	{
		printf("Stack is empty,nothing to print!\n");
		return;
	}
	for (int i = 0; i <= S.top; i++)
	{
		printf("%d ", S.data[i]);
	}
	printf("\n");
}

int main()
{
	SqStack S;
	InitStack(S);
	Push(S, 1);
	Push(S, 2);
	Push(S, 3);
	Push(S, 4);
	Push(S, 5);
	Push(S, 6);
	Push(S, 7);
	Push(S, 8);
	Push(S, 9);
	Push(S, 10);

	//测试栈
	for (int i = 0; i < MAdata_x_SIZE; i++)
	{
		if(S.top == -1)
			break;
		PrintStack(S);
		ElementType y;
		GetTop(S,y);
		printf("Top element is %d\n", y);
		Pop(S, y);
		printf("Pop element is %d\n", y);
		printf("After pop, stack is:\n");
		PrintStack(S);
		printf("\n");
	}

	return 0;
}

由链表发展而来,使用零散内存空间

1. 链栈定义

完全继承链表定义形式

1
2
3
4
5
6
7
8
9
10
11
#define ElemType int

typedef struct LinkStack
{
	ElemType data;
	struct LinkStack* next;
}*LS;
int main()
{
	LS L;
}

2. 链栈初始化

由于链表仅能由头结点开始遍历的特性,考虑到后续操作,链栈最佳初始化方案为头插法

1
2
3
4
5
6
7
8
9
void createStack(LS &L)
{
	LS p;
	ElemType x = 0;
	//头结点
	L = (LS)malloc(sizeof(struct LinkStack));
	L->data = x;
	L->next = nullptr;//后续第一个进入栈的节点将指向空,当栈为空时,next指向空
}

3.栈的状态

链栈没必要设置上限,除非是大数据流进入,否则零散利用内存的分配方式几乎不可能将内存占满

1
2
3
4
5
6
7
bool isEmpty(LS L)//当栈为空时,next指向空
{
	if (L->next == nullptr)
		return true;
	else
		return false;
}

4. 入栈

算法与头插法创建链表相同

1
2
3
4
5
6
7
8
void push(LS& L, ElemType x)
{
	LS p;
	p = (LS)malloc(sizeof(struct LinkStack));
	p->data = x;
	p->next = L->next;
	L->next = p;
}

5.出栈

调用并删除链表中第一个结点

1
2
3
4
5
6
7
8
9
10
11
12
13
14
bool pop(LS& L, ElemType& x)
{
	LS p;
	if (L->next == nullptr)
	{
		printf("Stack is empty!\n");
		return false;
	}
	p = L->next;
	x = p->data;
	L->next = p->next;
	free(p);
	return true;
}

6. 获取栈顶数据

1
2
3
4
5
6
7
8
9
10
bool getTop(LS L, ElemType& x)
{
	if (L->next == nullptr)
	{
		printf("Stack is empty!\n");
		return false;
	}
	x = L->next->data;
	return true;
}

链栈总体代码

链栈总体代码 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
#include <stdio.h>
#include <stdlib.h>
#include <string.h>

#define ElemType int

typedef struct LinkStack
{
	ElemType data;
	struct LinkStack* next;
}*LS;

void createStack(LS &L)
{
	LS p;
	ElemType x = 0;
	//头结点
	L = (LS)malloc(sizeof(struct LinkStack));
	L->data = x;
	L->next = nullptr;//后续第一个进入栈的节点将指向空,当栈为空时,next指向空

}

bool isEmpty(LS L)
{
	if (L->next == nullptr)
		return true;
	else
		return false;
}

void push(LS& L, ElemType x)
{
	LS p;
	p = (LS)malloc(sizeof(struct LinkStack));
	p->data = x;
	p->next = L->next;
	L->next = p;
}

bool pop(LS& L, ElemType& x)
{
	LS p;
	if (L->next == nullptr)
	{
		printf("Stack is empty!\n");
		return false;
	}
	p = L->next;
	x = p->data;
	L->next = p->next;
	free(p);
	return true;

}

bool getTop(LS L, ElemType& x)
{
	if (L->next == nullptr)
	{
		printf("Stack is empty!\n");
		return false;
	}
	x = L->next->data;
	return true;
}

void printStack(LS L)
{
	while (L->next!= nullptr)
	{
		printf("%d ", L->next->data);
		L = L->next;
	}
	printf("\n");
}

int main()
{
	LS L;
	createStack(L);
	push(L, 1);
	push(L, 2);
	push(L, 3);
	push(L, 4);
	printStack(L);

	ElemType x;
	pop(L, x);
	printf("poped element is %d\n", x);
	printStack(L);

	getTop(L, x);
	printf("top element is %d\n", x);
	printStack(L);

	return 0;
}

队列（Queue）

队列是一种先进先出（FIFO）的数据结构。队列中元素只能从一端进入（队尾），从另一端移除（队头）。常用操作包括：

  • enqueue：将元素加入队尾。
  • dequeue：将队头元素移除。
  • peek：查看队头元素。

队列的应用：广泛用于任务调度、广度优先搜索、数据缓冲等场景。

循环(顺序)队列(SquenceQueue)

1. 创建队列

循环队列又一个自定义的数组和队首与队尾两个逻辑指针构成

1
2
3
4
5
6
7
8
9
#define MAX_SIZE 5
#define ElementType int

typedef struct
{
	ElementType data[MAX_SIZE];
	int front, rear;  
} SquenceQueue;
//在循环队列中，data[SQ.rear]中的SQ.rear的值

2. 队列初始化

规定队列首尾标相等时为空

1
2
3
4
5
6
7
8
void InitQueue(SquenceQueue& SQ)
{
	SQ.front = SQ.rear = 0;
}
int main()
{
	SquenceQueue SQ;
}

3. 入队

循环队列核心算法 :

(SQ.rear + 1) % MAX_SIZE算法实现了索引循环的功能,且SQ.rear + 1避免了在数组被占满时尾标与头标重合的情况,即组下标越界，使得队列满时队首和队尾重合，再插入元素时会覆盖队首元素

该算法规定队首和队尾相等时为空,(SQ.rear + 1) % MAX_SIZE的存在SQ.rear和SQ.front的取值范围为[0,MAX_SIZE-1],构造体中的数组最后一位的被索引跳过,该存储单元值为0,且不会被调用

1
2
3
4
5
6
7
8
9
10
11
bool EnQueue(SquenceQueue& SQ,ElementType value)
{
	if ((SQ.rear + 1) % MAX_SIZE == SQ.front) //队尾标加1并向队列长度取余，等于队头，表示队列已满   
	{                                         
		printf("Queue is full!\n");           
		return false;                         
	}
	SQ.data[SQ.rear] = value;
	SQ.rear = (SQ.rear + 1) % MAX_SIZE; //当队尾标移动到倒数第二个位置时表示队列已满，向队列长度取余，使队尾标归零
	return true;
}

4. 出队

与入队原理相同

1
2
3
4
5
6
7
8
9
10
11
bool DeQueue(SquenceQueue& SQ, ElementType& value)
{
	if (SQ.front == SQ.rear) //队列为空，队头和队尾重合
	{
		printf("Queue is empty!\n");
		return false;
	}
	value = SQ.data[SQ.front];
	SQ.front = (SQ.front + 1) % MAX_SIZE; //队头向队列长度取余，使队头标归零
	return true;
}

5. 查看队首元素

1
2
3
4
5
6
7
8
9
10
11
bool peek(SquenceQueue SQ, ElementType& value)
{
	if (SQ.front == SQ.rear) //队列为空，队头和队尾重合
	{
		printf("Queue is empty!\n");
		return false;
	}
	return false;
	value = SQ.data[SQ.front];
	return true;
}

循环队列总体代码

循环队列总体代码 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
#include <stdio.h>
#include <stdlib.h>
#include <string.h>

#define MAX_SIZE 5
#define ElementType int

typedef struct
{
	ElementType data[MAX_SIZE];
	int front, rear;  
} SquenceQueue;
//在循环队列中，data[SQ.rear]中的SQ.rear的值

void InitQueue(SquenceQueue& SQ)
{
	SQ.front = SQ.rear = 0;
}

bool EnQueue(SquenceQueue& SQ,ElementType value)
{
	if ((SQ.rear + 1) % MAX_SIZE == SQ.front) //队尾标加1并向队列长度取余，等于队头，表示队列已满   
	{                                         
		printf("Queue is full!\n");           //
		return false;                         
	}
	SQ.data[SQ.rear] = value;
	SQ.rear = (SQ.rear + 1) % MAX_SIZE; //当队尾标移动到倒数第二个位置时表示队列已满，向队列长度取余，使队尾标归零
	return true;
}

bool DeQueue(SquenceQueue& SQ, ElementType& value)
{
	if (SQ.front == SQ.rear) //队列为空，队头和队尾重合
	{
		printf("Queue is empty!\n");
		return false;
	}
	value = SQ.data[SQ.front];
	SQ.front = (SQ.front + 1) % MAX_SIZE; //队头向队列长度取余，使队头标归零
	return true;
}

void PrintQueue(SquenceQueue SQ)
{
	if (SQ.front == SQ.rear) //队列为空，队头和队尾重合
	{
		printf("Queue is empty!\n");
		return;
	}

	for (int i = SQ.front; i != SQ.rear; i = (i + 1) % MAX_SIZE)
	{
		printf("%d ", SQ.data[i]);
	}
	printf("\n");
}

bool peek(SquenceQueue SQ, ElementType& value)
{
	if (SQ.front == SQ.rear) //队列为空，队头和队尾重合
	{
		printf("Queue is empty!\n");
		return false;
	}
	return false;
	value = SQ.data[SQ.front];
	return true;
}



int main_SQ()
{
	SquenceQueue SQ;
	InitQueue(SQ);
	EnQueue(SQ, 11);
	EnQueue(SQ, 22);
	EnQueue(SQ, 33);	
	EnQueue(SQ, 44);
	EnQueue(SQ, 55);
	PrintQueue(SQ);

	ElementType testvalue;
	DeQueue(SQ, testvalue);
	printf("DeQueue value is %d\n", testvalue);
	PrintQueue(SQ);

	DeQueue(SQ, testvalue);
	printf("DeQueue value is %d\n", testvalue);
	PrintQueue(SQ);

	EnQueue(SQ, 66);
	PrintQueue(SQ);
	return 0;
}

链队列(LinkQueue)

链队列由一个单链表和分别指代首尾的两个指针构成,用两个构造体分别构造单链表和首尾指针组

1. 构建链队列

1
2
3
4
5
6
7
8
9
10
11
12
13
#define ElementType int

typedef struct LinkQueueNode
{
    ElementType data;
    LinkQueueNode *next;
} LQN;

typedef struct LinkQueuePointers
{
    LQN *front;
    LQN *rear;
} LQP;

1. 初始化链队列

由于构造体LinkQueuePointers包含了用于指向LinkQueueNode的指针,因此只需创LinkQueuePointers的实例即可通过内置的指针来向内存申请空间

注意 : (LQN*)malloc(sizeof(struct LinkQueuePointers));这行代码的含义是向内存空间申请一个大小为两个指针空间,且这连个指针式用于指向构造体LinkQueuePointers的

1
2
3
4
5
6
7
8
9
10
11
void InitQueue(LQP &P)
{
    P.front = P.rear = (LQN*)malloc(sizeof(struct LinkQueuePointers));
    P.front->next = NULL;

}

int main()
{
    LQP P;
}

1. 入队

单链表尾插法入队,链表在内存空间足够大的情况下无需考虑长度上限问题

1
2
3
4
5
6
7
8
void EnQueue(LQP& P, ElementType x)
{
    LQN *newp = (LQN*)malloc(sizeof(struct LinkQueuePointers));   
    newp->data = x;
    P.rear->next = newp;//尾指针的next指向新节点
    P.rear = newp; //尾指针向后移动
    newp->next = nullptr; //此时尾节点更新,需设置为节点next为空
}

1. 出队

  1. 判断队列是否为空
  2. 拿到第一个结点的数据并断链和释放内存
  3. 考虑当取出最后一个结点元素时,尾指针与头指针复位的问题
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
bool DeQueue(LQP& P, ElementType& x)
{
    if (P.front == P.rear) //判断队列是否为空
    {
        printf("Queue is Empty,nothing can DeQueue");
        return false;
    }

    LQN* dep = P.front->next; //获取队首地址
    x = dep->data; //获取队首数据
    P.front->next = dep->next; //队首指针指向取出元素的节点的后面的节点

    if (P.rear == dep) //当取出的元素是最后一个元素时,使rear指针指向front指针,即队列为空
    {
        P.rear = P.front;
    }
    free(dep);
    return true;
}

1. 查看队首元素

1
2
3
4
5
6
7
8
9
10
11
12
bool PeekQueue(LQP P, ElementType &x)
{
    if (P.front == P.rear) //判断队列是否为空
    {
        printf("Queue is Empty,nothing can DeQueue");
        return false;
    }

    LQN* peekp = P.front->next; //获取队首地址
    x = peekp->data; //获取队首数据
    return true;
}

链式队列总体代码

链式队列总体代码 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
#include <stdio.h>
#include <stdlib.h>
#include <string.h>

#define ElementType int

typedef struct LinkQueueNode
{
    ElementType data;
    LinkQueueNode *next;
} LQN;

typedef struct LinkQueuePointers
{
    LQN *front;
    LQN *rear;
} LQP;

//采用尾插法建立链队列,规 定链尾为rear指针,链头为front指针
//入队时,将新结点p插入rear指针后面,然后将rear指针指向新结点p
//出队时,将front指针指向front指针后面的结点,并返回其数据
//判空时,若front指针为空,则队列为空,否则不为空

void InitQueue(LQP &P)
{
    P.front = P.rear = (LQN*)malloc(sizeof(struct LinkQueuePointers));
    P.front->next = nullptr;

}

void EnQueue(LQP& P, ElementType x)
{
    LQN *newp = (LQN*)malloc(sizeof(struct LinkQueuePointers));   
    newp->data = x;
    P.rear->next = newp;//尾指针的next指向新节点
    P.rear = newp; //尾指针向后移动
    newp->next = nullptr; //此时尾节点更新,需设置为节点next为空
}

bool DeQueue(LQP& P, ElementType& x)
{
    if (P.front == P.rear) //判断队列是否为空
    {
        printf("Queue is Empty,nothing can DeQueue");
        return false;
    }

    LQN* dep = P.front->next; //获取队首地址
    x = dep->data; //获取队首数据
    P.front->next = dep->next; //队首指针指向取出元素的节点的后面的节点

    if (P.rear == dep) //当取出的元素是最后一个元素时,使rear指针指向front指针,即队列为空
    {
        P.rear = P.front;
    }
    free(dep);
    return true;
}

bool PeekQueue(LQP P, ElementType &x)
{
    if (P.front == P.rear) //判断队列是否为空
    {
        printf("Queue is Empty,nothing can DeQueue");
        return false;
    }

    LQN* peekp = P.front->next; //获取队首地址
    x = peekp->data; //获取队首数据
    return true;
}

void PrintQueue(LQP P)
{
    LQN* p = P.front->next;
    while (p!= NULL)
    {
        printf("%d ", p->data);
        p = p->next;
    }
    printf("\n");   
}


int main()
{
    LQP P;

    InitQueue(P);
    EnQueue(P, 1);
    EnQueue(P, 2);
    EnQueue(P, 3);
    EnQueue(P, 4);
    EnQueue(P, 5);

    PrintQueue(P);

    ElementType x = 0;
    DeQueue(P, x);
    printf("dequeue is %d\n", x);
    PrintQueue(P);

    DeQueue(P, x);
    printf("dequeue is %d\n", x);
    PrintQueue(P);

    EnQueue(P, 6);
    PrintQueue(P);

    PeekQueue(P, x);
    printf("front of queue is %d\n", x);
    return 0;
}

树

二叉树(BinaryTree)

二叉树是一种树形数据结构，其中每个节点最多有两个子节点，称为左子节点和右子节点。二叉树具有层次关系，广泛用于数据组织和处理。

定义二叉树

二叉树主体由两个指针和一个数据组成,但构建二叉树还需要队列的辅助,采用链式队列为优

1
2
3
4
5
6
7
8
9
10
11
12
13
14
typedef char BT_ElemType;

typedef struct BiTreeNode
{
    BT_ElemType data;
    struct BiTreeNode *lchild, *rchild;
} BiTreeNode, *BiTree;

typedef struct BiTreeTagList //指针构造体,用于辅助构建二叉树
{
    BiTree p; //指向二叉树节点的指针
    struct BiTreeTagList *p_next; //指向按顺序进入二叉树的下一个节点的指针(指针的指针)
    //用于在双亲结点构建完成后对孩子结点进行孙子结点的构建
}*BiTreeTag;

层次创建二叉树

依照输入字符的顺序依次从上到下从左到右插入二叉树中

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
void BiTreeCreate_by_InputChar(BiTree &root)
{
    root = NULL; //指向树的根节点
    BiTree pnew; //指向新创建的树节点,用于构建二叉树
    char c;
    BiTreeTag phead = NULL, ptail = NULL; //分别指向辅助构建二叉树的指针链表的头和尾
    BiTreeTag listpnew = NULL; //指向辅助构建二叉树的指针链表中新创建的节点(链表的新元素),用于构建二叉树的辅助指针链表
    BiTreeTag pcur = NULL; //指向正在处理的辅助构建二叉树的指针链表的元素


    while (scanf_s("%c", &c))
    {
        if (c == '\n')
        {
            break; //换行符,表示输入结束
        }

        pnew = (BiTree)calloc(1, sizeof(BiTreeNode));
        //calloc分配内存,语法为:void *calloc(size_t num, size_t size);
        //calloc分配的内存空间,其大小为num*size字节,并初始化为0,即新建的节点的左右孩子指针都为NULL

        pnew->data = c; //为新创建的节点赋值

        listpnew = (BiTreeTag)calloc(1, sizeof(BiTreeTag));
        //在第一次输入值时作为辅助链表的头指针
        //在第二次输入值以后该指针是用于给辅助链表中的指针传值用的中间量

        listpnew->p = pnew; //为新创建的节点指针赋值,此时辅助指针链表得到了目前正在进行树节点构建的节点的指针值

        if (NULL == root)
        {
            root = pnew; //如果树还没有根节点,则为根节点赋值
            phead = listpnew; //为辅助指针链表的头指针赋值
            ptail = listpnew; //为辅助指针链表的尾指针也赋值
            pcur = listpnew; //pcur指向当前正在处理的辅助指针链表的元素

        }
        else
        {
            ptail->p_next = listpnew; //如果树已经有根节点,则将新创建的节点指针插入到辅助指针链表的尾部
            ptail = listpnew; //尾指针后移
            if (pcur->p->lchild == NULL) //pcur->p代表正在被加入孩子节点的节点的指针,即pnew
            {
                pcur->p->lchild = pnew; //为pcur->p的左孩子指针赋值
            }
            else if (pcur->p->rchild == NULL)
            {
                pcur->p->rchild = pnew; //为pcur->p的右孩子指针赋值
                //此时pcur->p已经完成了左右孩子的构建,pcur指向下一个待处理的辅助指针链表的元素
                pcur = pcur->p_next; //pcur指向下一个待处理的辅助指针链表的元素
            }

        }

    }
}

先序遍历(深度优先遍历)

1
2
3
4
5
6
7
8
//先序遍历
void PreOrder(BiTree root)
{
    if (root == NULL) return;
    printf("%c ", root->data); //先序遍历,根节点->左子树->右子树
    PreOrder(root->lchild);
    PreOrder(root->rchild);
}

中序遍历

1
2
3
4
5
6
7
8
//中序遍历
void InOrder(BiTree root)
{
    if (root == NULL) return;   
    InOrder(root->lchild); //左子树->根节点->右子树
    printf("%c ", root->data);
    InOrder(root->rchild);
}

后序遍历

1
2
3
4
5
6
7
8
//后序遍历
void PostOrder(BiTree root)
{
    if (root == NULL) return;
    PostOrder(root->lchild); //左子树->右子树->根节点
    PostOrder(root->rchild);
    printf("%c ", root->data);
}

层序遍历

需要辅助队列进行打印操作,这里使用的头文件来引用ListQueue的数据结构和方法

  1. 节点入队
  2. 打印并出队
  3. 判断出队的节点左右孩子是否为空,不为空则使其左右孩子入队,为空则继续
  4. 返回 1
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
//层序遍历二叉树
void LevelOrder(BiTree root)
{
    LQP Q; //队列
    BiTree p; //指向当前节点
    InitQueue(Q);
    EnQueue(Q,root);
    while (!IsEmpty(Q))// !bool等于对bool值取反
    {
        DeQueue(Q, p); //出队 p承接当前出队的节点
        putchar(p->data); //打印当前节点 putchar(p->data) = printf("%c", p->data)
        if (p->lchild != NULL)
        {
            EnQueue(Q, p->lchild); //左孩子入队
        }
        if (p->rchild != NULL)
        {
            EnQueue(Q, p->rchild); //右孩子入队
        }
    }
}
头文件和队列方法

头文件

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
#pragma once
#include <stdio.h>
#include <stdlib.h>
#include <string.h>


typedef char BT_ElemType;
typedef struct BiTreeNode
{
    BT_ElemType data;
    struct BiTreeNode* lchild, * rchild;
} BiTreeNode, *BiTree;

typedef struct BiTreeTagList //指针构造体,用于辅助构建二叉树
{
    BiTree p; //指向二叉树节点的指针
    struct BiTreeTagList* p_next; //指向按顺序进入二叉树的下一个节点的指针(指针的指针)
    //用于在双亲结点构建完成后对孩子结点进行孙子结点的构建
}*BiTreeTag;




typedef BiTree ElementType;
typedef struct LinkQueueNode
{
    ElementType data;
    LinkQueueNode* next;
} LQN;
typedef struct LinkQueuePointers
{
    LQN* front;
    LQN* rear;
} LQP;

//int fuc_print(int f);  // 函数声明
void InitQueue(LQP& P);
void EnQueue(LQP& P, ElementType x);
bool IsEmpty(LQP P);
bool DeQueue(LQP& P, ElementType& x);


队列方法

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
void InitQueue(LQP &P)
{
    P.front = P.rear = (LQN*)malloc(sizeof(struct LinkQueuePointers));
    P.front->next = nullptr;

}

void EnQueue(LQP& P, ElementType x)
{
    LQN *newp = (LQN*)malloc(sizeof(struct LinkQueuePointers));   
    newp->data = x;
    P.rear->next = newp;//尾指针的next指向新节点
    P.rear = newp; //尾指针向后移动
    newp->next = nullptr; //此时尾节点更新,需设置为节点next为空
}

bool IsEmpty(LQP P)
{
    return P.front == P.rear; // 队列为空返回 true，否则返回 false
}


bool DeQueue(LQP& P, ElementType& x)
{
    if (P.front == P.rear) //判断队列是否为空
    {
        printf("Queue is Empty,nothing can DeQueue");
        return false;
    }

    LQN* dep = P.front->next; //获取队首地址
    x = dep->data; //获取队首数据
    P.front->next = dep->next; //队首指针指向取出元素的节点的后面的节点

    if (P.rear == dep) //当取出的元素是最后一个元素时,使rear指针指向front指针,即队列为空
    {
        P.rear = P.front;
    }
    free(dep);
    return true;
}

二叉树创建与遍历总体代码

二叉树创建与遍历总体代码 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
#include "C_L_Header.h"

typedef char BT_ElemType;
typedef struct BiTreeNode
{
    BT_ElemType data;
    struct BiTreeNode* lchild, * rchild;
} BiTreeNode, *BiTree;

typedef struct BiTreeTagList //指针构造体,用于辅助构建二叉树
{
    BiTree p; //指向二叉树节点的指针
    struct BiTreeTagList* p_next; //指向按顺序进入二叉树的下一个节点的指针(指针的指针)
    //用于在双亲结点构建完成后对孩子结点进行孙子结点的构建
}*BiTreeTag;
            

void BiTreeCreate_by_InputChar(BiTree &root)
{
    root = NULL; //指向树的根节点
    BiTree pnew; //指向新创建的树节点,用于构建二叉树
    char c;
    BiTreeTag phead = NULL, ptail = NULL; //分别指向辅助构建二叉树的指针链表的头和尾
    BiTreeTag listpnew = NULL; //指向辅助构建二叉树的指针链表中新创建的节点(链表的新元素),用于构建二叉树的辅助指针链表
    BiTreeTag pcur = NULL; //指向正在处理的辅助构建二叉树的指针链表的元素


    while (scanf_s("%c", &c))
    {
        if (c == '\n')
        {
            break; //换行符,表示输入结束
        }

        pnew = (BiTree)calloc(1, sizeof(BiTreeNode));
        //calloc分配内存,语法为:void *calloc(size_t num, size_t size);
        //calloc分配的内存空间,其大小为num*size字节,并初始化为0,即新建的节点的左右孩子指针都为NULL

        pnew->data = c; //为新创建的节点赋值

        listpnew = (BiTreeTag)calloc(1, sizeof(BiTreeTag));
        //在第一次输入值时作为辅助链表的头指针
        //在第二次输入值以后该指针是用于给辅助链表中的指针传值用的中间量

        listpnew->p = pnew; //为新创建的节点指针赋值,此时辅助指针链表得到了目前正在进行树节点构建的节点的指针值

        if (NULL == root)
        {
            root = pnew; //如果树还没有根节点,则为根节点赋值
            phead = listpnew; //为辅助指针链表的头指针赋值
            ptail = listpnew; //为辅助指针链表的尾指针也赋值
            pcur = listpnew; //pcur指向当前正在处理的辅助指针链表的元素

        }
        else
        {
            ptail->p_next = listpnew; //如果树已经有根节点,则将新创建的节点指针插入到辅助指针链表的尾部
            ptail = listpnew; //尾指针后移
            if (pcur->p->lchild == NULL) //pcur->p代表正在被加入孩子节点的节点的指针,即pnew
            {
                pcur->p->lchild = pnew; //为pcur->p的左孩子指针赋值
            }
            else if (pcur->p->rchild == NULL)
            {
                pcur->p->rchild = pnew; //为pcur->p的右孩子指针赋值
                //此时pcur->p已经完成了左右孩子的构建,pcur指向下一个待处理的辅助指针链表的元素
                pcur = pcur->p_next; //pcur指向下一个待处理的辅助指针链表的元素
            }

        }

    }
}

//先序遍历
void PreOrder(BiTree root)
{
    if (root == NULL) return;
    printf("%c ", root->data); //先序遍历,根节点->左子树->右子树
    PreOrder(root->lchild);
    PreOrder(root->rchild);
}

//中序遍历
void InOrder(BiTree root)
{
    if (root == NULL) return;   
    InOrder(root->lchild); //左子树->根节点->右子树
    printf("%c ", root->data);
    InOrder(root->rchild);
}

//后序遍历
void PostOrder(BiTree root)
{
    if (root == NULL) return;
    PostOrder(root->lchild); //左子树->右子树->根节点
    PostOrder(root->rchild);
    printf("%c ", root->data);
}

// 打印树状二叉树
void PrintTree(BiTree root, const char* prefix, int isLeft) {
    if (root == NULL) {
        return;
    }

    // 打印当前节点，显示前缀与分支符号
    printf("%s", prefix);
    printf(isLeft ? "├── " : "└── ");
    printf("%c\n", root->data);

    // 新的前缀
    char newPrefix[100];
    snprintf(newPrefix, sizeof(newPrefix), "%s%s", prefix, isLeft ? "│   " : "    ");

    // 递归打印左右子树
    if (root->lchild || root->rchild) {
        PrintTree(root->rchild, newPrefix, 1);
        PrintTree(root->lchild, newPrefix, 0);
        
    }
}

//层序遍历二叉树
void LevelOrder(BiTree root)
{
    LQP Q; //队列
    BiTree p; //指向当前节点
    InitQueue(Q);
    EnQueue(Q,root);
    while (!IsEmpty(Q))// !bool等于对bool值取反
    {
        DeQueue(Q, p); //出队 p承接当前出队的节点
        putchar(p->data); //打印当前节点 putchar(p->data) = printf("%c", p->data)
        if (p->lchild != NULL)
        {
            EnQueue(Q, p->lchild); //左孩子入队
        }
        if (p->rchild != NULL)
        {
            EnQueue(Q, p->rchild); //右孩子入队
        }
    }
}

int main() {
    BiTree Btree01;

    // 输入二叉树
    printf("请输入二叉树节点序列（以换行结束）：\n");
    BiTreeCreate_by_InputChar(Btree01);

    // 先序遍历
    printf("先序遍历结果:\n");
    PreOrder(Btree01);
    printf("\n");

    // 中序遍历
    printf("中序遍历结果:\n");
    InOrder(Btree01);
    printf("\n");

    // 后序遍历
    printf("后序遍历结果:\n");
    PostOrder(Btree01);
    printf("\n");

    // 层序遍历
    printf("层序遍历结果:\n");
    LevelOrder(Btree01);
    printf("\n");

    // 打印树状结构
    printf("树状打印结果:\n");
    PrintTree(Btree01, "", 0);


    return 0;
}

哈夫曼树(Huffman Tree)

以后再来写

哈夫曼编码

  • Title: Data_structures_BaseDataType
  • Author: Slience_Displace
  • Created at: 2024-11-28 00:00:00
  • Updated at: 2024-12-19 17:33:01
  • Link: https://mikumikudaifans.github.io/Displace.github.io/2024/11/28/DataStructuresBase/
  • License: This work is licensed under CC BY-NC-SA 4.0.
 Comments
On this page
Data_structures_BaseDataType
  1. 时间复杂度&空间复杂度
    1. 时间复杂度(time complexity)
    2. 空间复杂度(space complexity)
  2. 线性表
    1. 顺序表(Sequence List)
    2. 单链表(Single Linked List)
  3. 栈 （Stack）
    1. 顺序栈(squencial stack)
    2. 链栈（Link Stack)
  4. 队列（Queue）
    1. 循环(顺序)队列(SquenceQueue)
    2. 链队列(LinkQueue)
  5. 树
    1. 二叉树(BinaryTree)
    2. 哈夫曼树(Huffman Tree)